Iнтегрування рацiональних функцiй
Вам слід познайомитись з методом інтегрування деяких раціональних функцій.
Якщо знаменник правильного раціонального дробу }{Q(x)})
можна подати у вигляді добутку лінійних множників, наприклад =(x-x_1)(x-x_2)(x-x_3),)
то дріб можна буде подати у вигляді суми дробів, тобто
Зводячи, в правій частині рівності, до спільного знаменника та прирівнявши в чисельниках лівої та правої частин коефіцієнти при однакових степенях, тобто застосовуючи метод невизначених коефіцієнтів, знаходимо 
, після чого замість вихідного дробу будемо інтегрувати суму отриманих найпростіших дробів. У випадку коли дріб неправильний, то попередньо необхідно виділити цілу частину.
Приклад 1. Знайти інтеграл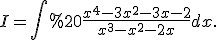 
Так як степінь чисельника вищий за степінь знаменника, тобто дріб неправильний, то розділивши чисельник на знаменник, виділимо цілу частину.
Тобто dx-%20\int%20\frac{(x+2)dx}{x(x-2)(x+1)}.)
Отриманий правильний дріб розкладемо на найпростіші:
Підставляючи по черзі в ліву та праву частини рівності значення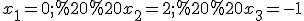 
(корені знаменника), отримаємо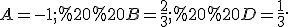 
Остаточно отримаємо
Немає коментарів:
Дописати коментар