Первісна та її властивості
Невизначений інтеграл
Якщо основне завдання диференціального числення завдання полягає в тому, щоб знайти похідну функції, то основне завдання інтегрального числення полягає у виконанні оберненого завдання. А саме: відшукати функцію, знаючи її похідну. Наприклад: часто, знаючи закон, за яким змінюється швидкість прямолінійного руху матеріальної точки, необхідно відшукати інформацію про закон її руху.
Означення. Функція )
називається первісною для функції )
на заданому проміжку, якщо для всіх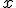 
з цього проміжку виконується рівність
Приклад. =\cos%20x)
,
Але, якщо функція )
є первісною для функції , то і +C)
(2) , де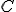 
- довільна константа, теж є первісною для .Справді,
Отже, якщо функція має одну первісну, то вона має нескінченну множину первісних.
Виникає запитання: Чи кожну первісну можна подати у вигляді (2)?
Відповідь на це запитання дає теорема:
Т. Якщо функція є однією з первісних для функції на заданому проміжку, то кожна інша первісна )
для на тому ж проміжку має вигляд
Доведення. Оскільки
За ознакою сталості маємо
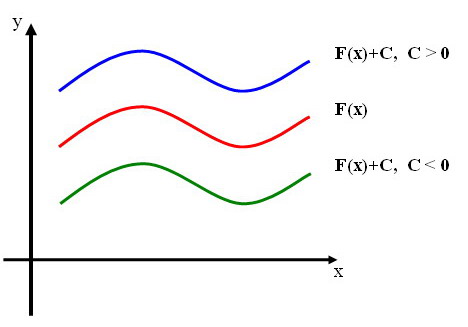
З геометричної точки зору ця теорема означає, що графік довільної первісної для отримується паралельним перенесенням графіка відомої кривої )
вздовж вісі ординат.
Означення. Множина всіх первісних для функції на даному проміжку називається невизначеним інтегралом для })
на цьому проміжку та познається
За означенням dx=F(x)+C})
. (3)
(3) показує, що задача відшукання первісних та невизначеного інтегралу для даної функції майже тотожні задачі, тому їх називають інтегруванням.
Знову виникає запитання: чи завжди можливе інтегрування?
Виявляється що ні, але якщо функція неперервна на проміжку, то первісна для неї на цьому проміжку обов'язково існує.
Властивості невизначеного інтегралу
T1. Якщо функція є первісною функції , а - первісна функції )
, то +G(x))
є первісною для +g(x).)
Доведення.
T2. Якщо є первісною для , а 
- константа, то )
є первісною для )
.
Доведення.
T3. Якщо є первісною для функції , а та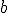 
- константи, причому 
, то )
є первісною для функції )
.
Доведення.
Корисно пам'ятати
 | |
1
| |
Приклади.
1. Знайти первісну функції 
.
Для 
.
Для 
.
За Т.1 однією із первісних буде =\frac{x^4}{4}-\frac{1}{x}.)
2. 
Так як однією із первісних функції 
є 
, то за Т.2 маємо
3. )
Однією із первісних для функції є , то за Т.3 маємо
Немає коментарів:
Дописати коментар