Означення визначеного інтегралу

Означення визначеного інтегралу

Площа криволінійної фігури (трапеції)

Задамо на відрізку 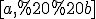 (  та 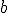 - скінченні числа ) невід'ємну неперервну функцію .

Поставимо задачу: необхідно розумно означити поняття площі фігури, обмеженої кривою , віссю 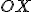, прямими  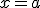та 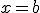 та обчислити цю площу.

Розіб'ємо відрізок 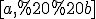 на 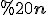 рівних частин точками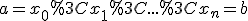 

або 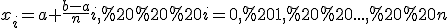 і отримаємо відрізки довжиною  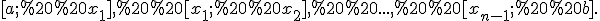Позначимо через  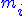та 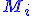відповідно найменше та найбільше значення функції  на відрізку 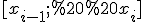, де .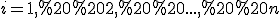

Очевидно, що площа 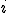-тої частини не менша за  та не більша .

Тому площа всієї криволінійної фігури не менша від суми 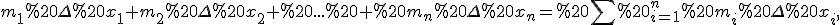 де 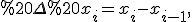 та не більша за суму  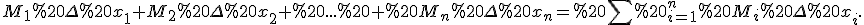Позначивши ці суми відповідно  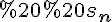та 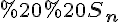 отримаємо, що площа фігури ( трапеції) задовольняє нерівності   .

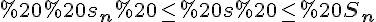В цій нерівності зліва стоїть площа східчастої фігури, яка міститься в даній криволінійній трапеції, а зліва - площа східчастої фігури, яка містить дану криволінійну трапецію.

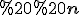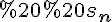Інтуїтивно зрозуміло, що при досить великому  площі  та 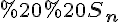 вказаних фігур мало чим відрізняються одна від одної та від площі криволінійної трапеції.

Означення. Нехай  - неперервна невід'ємна функція. Тоді, якщо границі послідовностей 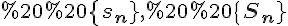 існують та рівні, то їх значення називається площею криволінійної трапеції.

На кожному відрізку 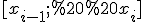 виберемо довільну точку  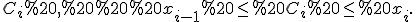Для неї буде правильною подвійна нерівність  де 

Кожну із нерівностей помножимо на 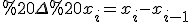 і отримані всі нерівності додамо.

Отримаємо

 

де сума  називається інтегральною сумою функції на відрізку .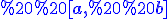

Якщо у співвідношенні (*) перейти до границі при 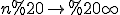 отримаємо, що границя інтегральної суми існує, не залежить від вибору точок  і дорівнює площі фігури

Означення. Нехай є функція  Якщо границя

існує та не залежить від вибору точок , то функція називається інтегровною на відрізку 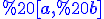, а границя називаєтьсявизначеним інтегралом від функції  на відрізку 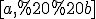 та позначається