Формула Ньютона-Лейбніца
Т. Якщо функція )
неперервна на відрізку 
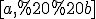, а функція )
є первісною для на 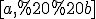, то справедлива формула
Доведення
Так як функції та )
є первісними для функції на відрізку 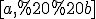, то різниця -F(x))
дорівнює деякій константі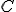 
на всьому проміжку , тобто
Спочатку покладемо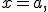 
а потім 
то отримаємо
Так як =0)
, то ,)
а тому =F(b)-F(a))
, де =\int_{a}^b%20f(x)dx.)
Теорему доведено.
Часто замість різниці -F(a),)
пишуть %20\%20|%20_a^b)
і тоді формула (1) приймає вигляд dx%20=F(x)%20\%20|%20_a^b)
.
Таким чином dx%20=\int_a^b%20dF(x)%20=F(x)%20\%20|%20_a^b=F(b)-F(a).)
Формула Ньютона – Лейбніца дозволяє обчислювати визначений інтеграл без інтегральної суми та граничного переходу в тих випадках, коли відомо хоча б одна первісна підінтегральної функції.
Розглянемо приклади застосування формули Ньютона-Лейбніца.
Пр 1. Обчислити Так як функція
Немає коментарів:
Дописати коментар