Використання формули Ньютона-Лейбніца
.
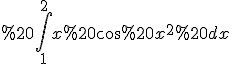Покладемо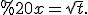
Необхідно кругом 
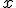замінити на 
.
.)
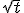Приклад 2. Обчислити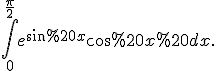
Нехай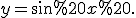
Маємо
=\int_0^{1}e^y%20dy=e^y|_0^1=e-1.)
Приклад 3. Обчислити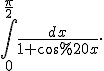 
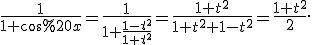Тепер обчислимо 
:
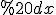%27dt=\frac{2}{1+t^2}dt.)
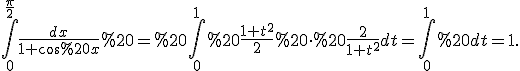
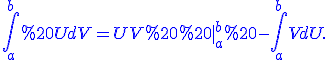
Приклад 1. Обчислити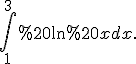
=3%20\ln%203-%20\int_1^3x\frac{1}{x}dx=3%20\ln%203-%20\int_1^3%20dx=3\ln%203%20-2.)
Приклад 2. Обчислити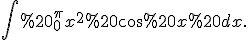 
Нехай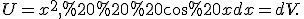
Тоді 
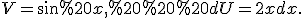
За формулою інтегрування частинами маємо:
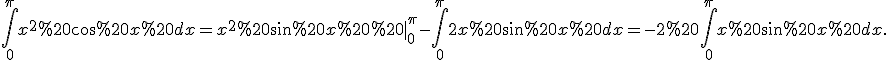
=-x\cos%20x|_0^{\pi}+\int_0^{\pi}%20\cos%20x%20dx=\pi+\sin%20x|_0^{\pi}=\pi.)
Таким чином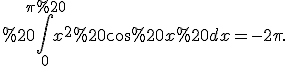
Метод заміни змінної та
метод інтегрування по частинах у
визначеному інтегралі
Обчислення визначеного інтегралу методом заміни змінної
Приклад 1. Обчислити Покладемо
Необхідно, також, змінити межі інтегрування. В нас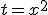 
, а тому в новому інтегралі межами інтегрування будуть 1 та 4. Таким чином
Приклад 2. Обчислити
Нехай
Маємо
Для знаходження невизначеного інтеграла від функції =\frac{1}{1+\cos%20x})
скористаємося підстановкою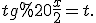 
Точніше кажучи, зробимо таку заміну змінної інтегрування: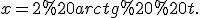 
Із формул тригонометрії слідує, що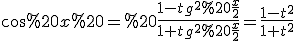 
, а тому
Знайдемо нові межі інтегрування. Так як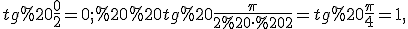 
то в новому інтегралі межами інтегрування будуть 0 та 1.
Таким чином,
Обчислення визначеного інтегралу методом інтегрування по частинах
Як відомо, формула інтегрування по частинах для невизначеного інтегралу доводиться інтегруванням рівності %27=UV%27+VU%27.)
Аналогічно доводиться формула інтегрування по частинах для визначеного інтегралу.
Т. Якщо функції ,%20\%20V(x))
мають неперервні похідні на відрізку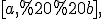 
то справджується формула , яка коротко може бути записана так:
(без доведення).
Формула інтегрування по частинах зводить обчислення одного інтегралу до обчислення другого.
Зрозуміле прагнення зробити так, щоб другий інтеграл був простішим за перший або зручнішим.Приклад 1. Обчислити
Покладемо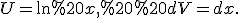 
Застосовуючи формулу інтегрування по частинах маємо:
Нехай
За формулою інтегрування частинами маємо:
До отриманого інтегралу знову застосуємо формулу інтегрування по частинах:
Таким чином
Немає коментарів:
Дописати коментар