Використання формули Ньютона-Лейбніца для обчислення площ фігур

Криволінійна трапеція та її площа


Формула Ньютона-Лейбніца.  Якщо F(x) - це первісна функція для неперервної  функції f(х)  на обмеженому проміжку [a; b] , то площа криволінійної трапеції дорівнює визначеному інтегралу, тобто конкретному числу, яке обчислюється за формулою: S=F(b)-F(a).



Завдання.

Вставте пропущені символи, щоб рівність була правильною.

Після виконання самостійної роботи учні перевіряють правильність виконання самостійної роботи, звіряючи написане в зошиті з правильними відповідями, що вкладені в заклеєний конверт, який лежить в кожному зошиті:

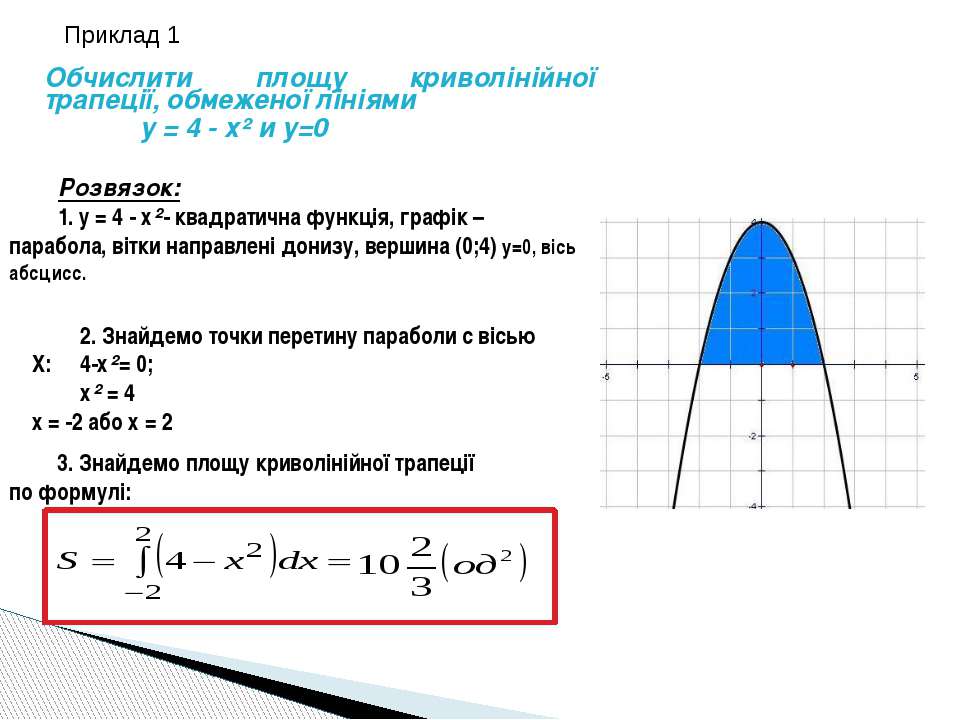
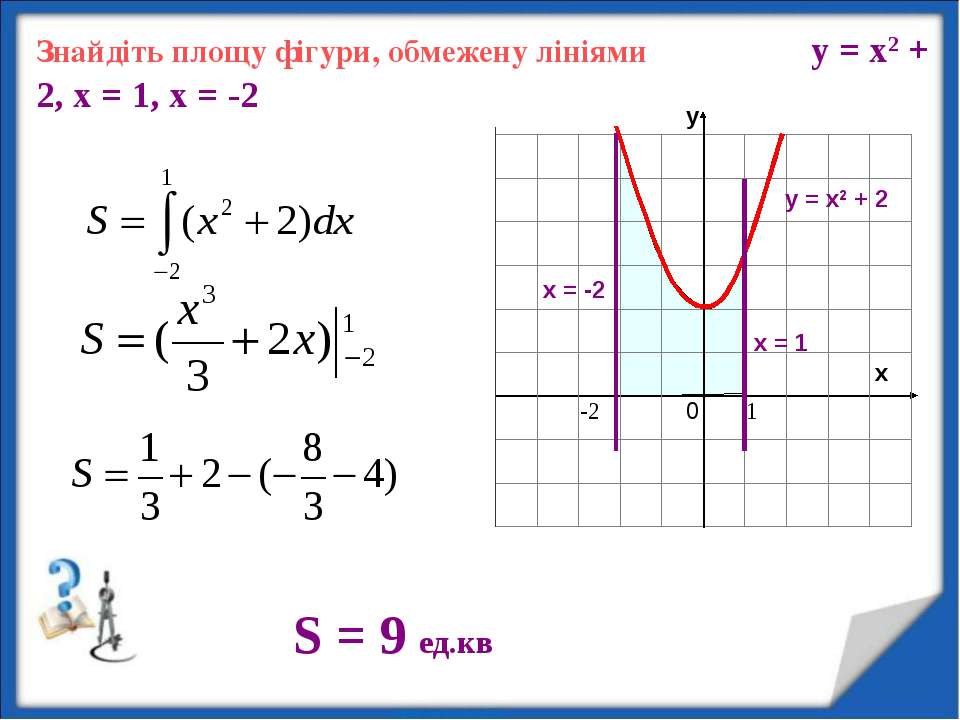
Завдання для осмислення теоретичного матеріалу

Поставте правильно напрямок від фігури до формули, завдяки якій можна обчислити її площу.

Обчислення об’єму тіла, утвореного обертанням графіка функції навколо вісі Ох:

 Обчислення об’єму тіла, утвореного обертанням графіка функції навколо вісі Оу:

А де саме визначений інтеграл застосовується у фізиці?

	Швидкість тіла v
	Заряд  q(t)
	Роботу при прямолінійному русі A1
	Кількість теплоти Q
	Робота при змінній потужності A2
	Координата тіла  x(t)
	Маса стержня  m(l)

Давайте розглянемо, коли нам може знадобитися визначений інтеграл при розв’язуванні задач з економіки?

Якщо f(t) – продуктивність праці в момент t, то

– обсяг продукції, яка випускається за проміжок часу [0; T].

Приклад. 

Продуктивність  праці  робітника протягом дня задається функцією z(t) = – 0,00645t² + 0,05t + 0,5 (грош. од./год), де t – час в годинах від початку роботи, 0 ≤ t ≤ 8. Знайти функцію Ǫ = Ǫ(t), яка показує обсяг продукції (у вартісному виразі) та його величину за робочий день.

Розв’язання:

Відповідь: 4,5 грош. од.

Завдання для самостійного опрацювання

І.Обчислити площу фігури, обмежену лініями, різними способами:

1) у = 2х + 1;  у = 0, у = 4 – х.

2) у = -3х + 2;  у = 2, у = 6 + х.

3) у = 3х - 2;  у = -2, у = -6 - х.

4) у = -х + 2;  у = 4, у = -2+ х.

5) у = sinх; у = 0, x =  /6, x =  /4.

6) у = cosх; у = 0, x = 0, x = p/2.

7) у = - sinх; у = 0, x = 0, x = p.

8) у = - cosх; у = 0, x = 0, x = 2p.

9) у = 2sinх; у = 0, x = p/6, x = p/3.

10) у = 3cosх; у = 0, x = 0, x = 3p/2.

11) у = 6sin2х; у = 0, x = p/6, x = p/3.

12) у = 3cos(0,5х); у = 0, x = 0, x = 3p/2.

13) у =1 - 2sin3х; у = 0, x = p/4, x = p/3.

14) у = 3 - 2cos2х; у = 0, x = p/3, x = p/2.

15) у = - х² + 2х + 6;  у = 6 – х.

16) у = - х² - 4х; у = 4 – х.

17) у = х² + 2х - 3; у = -3 + х.

18) у =  - х² -4х - 1;  у =  х² + 2х - 5.

19) у = х² + 4х + 4; у = -4 + х².

20) у = - х² + 2х + 6;  у = х² + 4х + 6.

21) у =  х² + 2х - 5;  у = - х² - 4х - 5.

22) у = х² + 2х -3; у = - х² - 2х -3.

23) у = (25 - х² )^0,5,   х = 0, у = 0.

24) у = (16 - х² )^0,5,   х = 0.

25) у = - (9 - х² )^0,5,   х = 0.

26) у = 4/х,   х = 4, у = 4.

27) у = х^0,5,   х = 9, у = 0.

28) у = -(-х)^0,5,   х = -4, у = 0.

29) у = 0,   у = 4, х = 4,  х = 0,  у = - 2+ х; у = 2+ х;   

30) у = х² - 2|х| -3; у = - х² - 2|х|  +3.

31) у = (2 - х )^0,5,   у = (x +2 )^0,5,   х = 6, у = 0.

32) у = -(1 - х )^0,5,   у = -(x +3 )^0,5,   х = 4, у = 0.

33) у = (2 - х )^0,5,   у = (4 - х )^0,5,   у = 0.

34) у = (1 - х )^0,5,   у = (x +4 )^0,5,   у = 0.

35) у = х²,   у = х³,   х = 0, х = 1.

36) у = -х³,   у = -х⁵,   х = 0, х = -1.

37) у = -х²,   у = -1/х,   х = 9, y = 0.