Олімпіада магічних головоломок

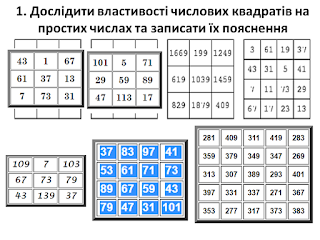
Способи узагальнення послідовності Фібоначчі

Перший спосіб узагальнення послідовностей Фібоначчі

Означення. Узагальненою послідовністю Фібоначчі 
 A_р(х₁, х₂, …, х_q )   р- ціле число,  q- натуральне число
із  q змінними   називають таку закономірність утворення чисел, котра задається рекурентною формулою у вигляді суми двох членів послідовності, які знаходяться на певній відстані один від одного:

                        A_р= A_р-1 + A_р-q,

де одразу відомі q-перших членів послідовності, а саме 

A₁= х₁, 

A₂= х₂, 

…, 

A_q= х_{q ,} 

де  { х₁, х₂, …, х_q } - дійсні числа, q- ціле число.

Приклади узагальнених послідовностей Фібоначчі:

A_р= A_р-1 + A_р-q, 1)Якщо q=2,  тоді A_р= A_р-1 + A_р-2, де

A₁=1;  

A₂=1;  

A₃=2;  

A₄=3, …  - послідовність Фібоначчі;

2)Якщо q=3,  тоді A_р= A_р-1 + A_р-3, де змінні члени  узагальненої послідовності Фібонначчи:

A₁=k;  

A₂=m;  

A₃=n;  

 де {k, m, n} - дійсні числа, р -ціле число,  тоді  отримаємо наступні члени послідовності із  змінними в обидві сторони, з додатним індексом або від'ємним індексом:

……………………….

A_-11=-8k+4m+n;

A_-10=k-8m +5n

A_-9=5k+m-3n;

A_-8=-3k+5m-2n;

A_-7=-2k-3m+3n

A_-6=3k-2m;

A_-5=3m-2n;

A_-4=n-2k;

A_-3=n-2m+k;

A_-2=k-n+m;

A_-1=m-k;

A₀=n-m;

A₁=k;  

A₂=m;  

A₃=n;   

A₄=n+k;

A₅=n+k+m;   

A₆=2n+k+m;  

A₇=3n+2k+m;    

A₈=4n+3k+2m;

A₉=6n+4k+3m;

A₁₀=9n+6k+4m;

A₁₁=13n+9k+6m;

…………………………..

 {k, m, n} - дійсні числа.

Другий спосіб узагальнення послідовностей Фібоначчі

В математиці, послідовностями Люка називають сімейство пар лінійних рекурентних послідовностей другого порядку, вперше розглянутих Едуардом Люка.

Послідовності Люка являють собою пари послідовностей ${\displaystyle \{U_{n}(P,Q)\}}$ и ${\displaystyle \{V_{n}(P,Q)\}}$, що задовольняють одному і тому ж рекурентному співвідношенню з коефіцієнтами P і Q:

${\displaystyle U_{0}(P,Q)=0,\quad U_{1}(P,Q)=1,\quad U_{n+2}(P,Q)=P\cdot U_{n+1}(P,Q)-Q\cdot U_{n}(P,Q),\,n\geq 0}$

${\displaystyle V_{0}(P,Q)=2,\quad V_{1}(P,Q)=P,\quad V_{n+2}(P,Q)=P\cdot V_{n+1}(P,Q)-Q\cdot V_{n}(P,Q),\,n\geq 0}$

Приклади

Деякі послідовності Люка носять власні імена:

• ${\displaystyle \{U_{n}(1,-1)\}}$ - числа Фібоначчі
• ${\displaystyle \{V_{n}(1,-1)\}}$ - числа Люка
• ${\displaystyle \{U_{n}(2,-1)\}}$ - числа Пелля
• ${\displaystyle \{V_{n}(2,-1)\}}$ - числа Пелля-Люка
• ${\displaystyle \{U_{n}(3,2)\}}$ - числа Мерсенна
• ${\displaystyle \{U_{n}(1,-2)\}}$ - числа Якобшталя

Характеристичним многочленом послідовностей Люка ${\displaystyle \{U_{n}(P,Q)\}}$ та ${\displaystyle \{V_{n}(P,Q)\}}$ є:

${\displaystyle x^{2}-P\cdot x+Q}$

Його дискримінант ${\displaystyle D=P^{2}-4Q}$ вважається не рівним нулю. Корені характеристичного многочлена

${\displaystyle \alpha ={\frac {P+{\sqrt {D}}}{2}}}$ и ${\displaystyle \beta ={\frac {P-{\sqrt {D}}}{2}}}$

можна використовувати для отримання явних формул:

${\displaystyle U_{n}(P,Q)={\frac {\alpha ^{n}-\beta ^{n}}{\alpha -\beta }}={\frac {\alpha ^{n}-\beta ^{n}}{\sqrt {D}}}}$

та

${\displaystyle V_{n}(P,Q)=\alpha ^{n}+\beta ^{n}.~}$

Обчислення значення золотого перетину

Золотий перетин ${\displaystyle \varphi }$ можна обчислити безпосередньо з означення:

${\displaystyle {\frac {a+b}{a}}={\frac {a}{b}}=\varphi \,.}$

Праве рівняння дає ${\displaystyle a=b\varphi \,}$. Підставляючи цю рівність у ліву частину:

${\displaystyle {\frac {b\varphi +b}{b\varphi }}={\frac {b\varphi }{b}}\,.}$

Скоротивши ${\displaystyle b\,}$ отримаємо:

${\displaystyle {\frac {\varphi +1}{\varphi }}=\varphi .}$

Помноживши обидві частини на ${\displaystyle \varphi \,}$ після перестановки отримаємо:

${\displaystyle \varphi ^{2}-\varphi -1=0.}$

Це квадратне рівняння має два розв'язки, один з яких є додатнім

${\displaystyle \varphi ={\frac {1+{\sqrt {5}}}{2}}\approx 1.61803\,39887\dots \,}$

Зв'язок із числами Фібоначчі

Спіраль Фібоначчі

Золотий перетин є границею відношення двох сусідніх членів у послідовності Фібоначчі:

${\displaystyle \lim _{n\to \infty }{\frac {F_{n+1}}{F_{n}}}=\varphi .}$

При цьому члени послідовності ${\displaystyle {\frac {F_{n+1}}{F_{n}}}}$ збігаються до ${\displaystyle \varphi \,}$ поперемінно: один елемент — знизу, наступний — зверху і т. д. Наприклад

${\displaystyle {\frac {F_{6}}{F_{5}}}={\frac {8}{5}}=1,6<\varphi <{\frac {F_{7}}{F_{6}}}={\frac {13}{8}}=1,625}$

Формула Біне виражає за допомогою ${\displaystyle \varphi \,}$ значення числа Фібоначчі ${\displaystyle F_{n}\,}$ в явному вигляді:

${\displaystyle F_{n}={\frac {\varphi ^{n}-(-\varphi )^{-n}}{\varphi -(-\varphi )^{-1}}}={\frac {\left({\frac {1+{\sqrt {5}}}{2}}\right)^{n}-\left({\frac {1-{\sqrt {5}}}{2}}\right)^{n}}{\sqrt {5}}}\approx {\frac {\varphi ^{n}}{\sqrt {5}}}\quad (n\geq 1).}$

Окрім цього, послідовні степені числа ${\displaystyle \varphi \,}$ задовільняють рекурентному співвідношенню ідентичному до чисел Фібоначчі:

${\displaystyle \varphi ^{n+2}=\varphi ^{n+1}+\varphi ^{n}.\,}$

Спіраль Фібоначчі (див. рисунок) є наближенням золотої спіралі.