Завдання на дослідження
властивостей чудових функцій:
Функцію f: R-->R назвемо чудовою
парного вигляду, якщо вона:
1) має лише нулі х1;
х2; х3; … хn, що явлються
парними числами;
2) приймає
значення х1; х2; х3; … хn лише при парних значеннях аргумента.
Функцію f: R-->R назвемо чудовою
непарного вигляду, якщо вона:
1) має лише нулі х1;
х2; х3; … хn, що явлються непарними
числами;
2) приймає
значення х1; х2; х3; … хn лише при непарних значеннях аргумента.
Функцію f: R-->R назвемо чудовою
непарно-парного вигляду, якщо вона:
1) має лише нулі х1;
х2; х3; … хn, що явлються непарними
числами;
2) приймає
значення х1; х2; х3; … хn лише при парних значеннях аргумента.
Функцію f: R-->R назвемо чудовою
парно-непарного вигляду, якщо вона:
1) має лише нулі х1;
х2; х3; … хn, що явлються
парними числами;
2) приймає
значення х1; х2; х3; … хn лише при непарних значеннях аргумента.
Обгрунтувати відповіді на запитання:
Чи існують квадратичні функції, що являються: 1)чудовою парного
вигляду; 2) чудовою непарного
вигляду; 3) чудовою непарно-парного вигляду; 4) чудовою парно-непарного вигляду?
Чи може парна
функція бути чудовою парного вигляду?
Чи може непарна
функція бути чудовою парного вигляду?
Чи може парна
функція бути чудовою непарного вигляду?
Чи може непарна
функція бути чудовою непарного вигляду?
Чи може парна
функція бути чудовою парно-непарного вигляду?
Чи може непарна
функція бути чудовою
парно-непарного вигляду?
Чи може парна
функція бути чудовою непарно-парного вигляду?
Чи може непарна
функція бути чудовою непарно-парного вигляду?
Чи можна стверджувати, що a(x)= a*f(x) - чудовo парного вигляду,
якщо а – дійсне ненульове число, f(x) - чудовo парного вигляду?
Чи можна стверджувати, що В(x)= af(x) +bg(x) - чудовo парного вигляду, якщо
1)а та b – дійсні ненульові числа;
2)функції g(x), f(x) - чудовo парного вигляду?



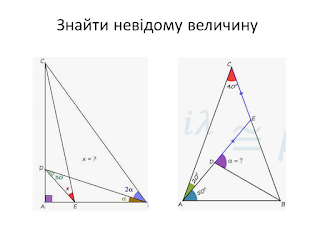
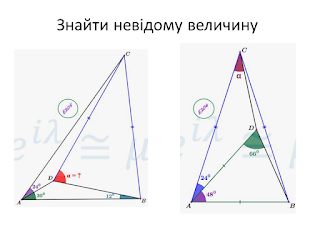





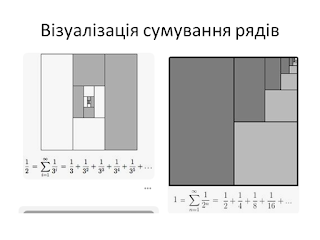











Немає коментарів:
Дописати коментар