ОЗНАЧЕННЯ
ПОХІДНОЇ
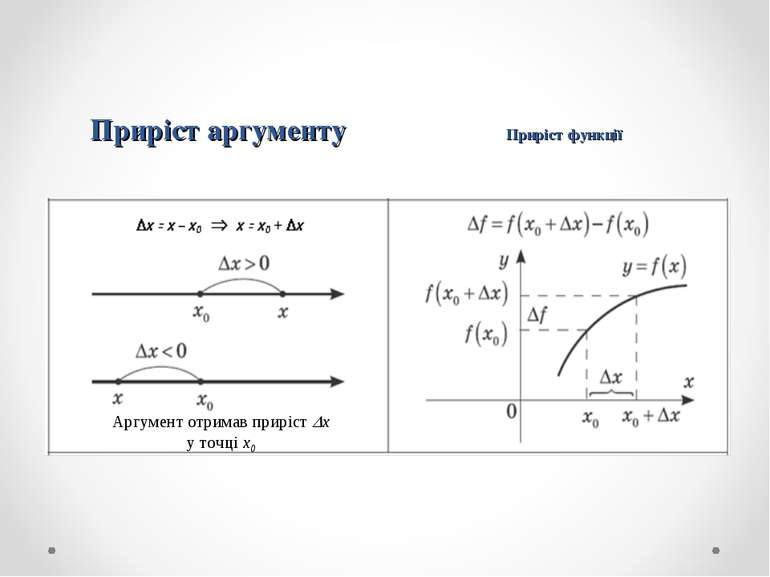
Нехай
задано
функцію формулою у = f(х).
Означення. Похідною
функції
у = f(х) в точці хo називається, границя відношення приросту функції Δf(хo)
в точці хo до приросту
аргументу Δх, коли приріст аргументу прямує до нуля
(можна позначити у ' або f '(х))




f '(х) = lim Δx
->0(f(хo + Δх) - f(хo))/Δх
Означення. Операція
знаходження похідної називається
диференціюванням.
Знайти відношення приросту функції до приросту аргументу
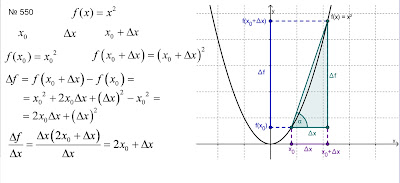
Знайти відношення приросту функції до приросту аргументу


Дотична до графіка функції і геометричний
зміст похідної
Означення. Дотичною до
кривої в даній точці М називається граничне положення січної МN, коли точка N наближається вздовж
кривої до точки М
k - кутовий коефіцієнт дотичної
k = tg φ = f '(хo) )
y = f(xо) + f '(xо) (x - xo) -
рівняння
дотичної до
графіка функції y = f(х) в точці з абсцисою хо.

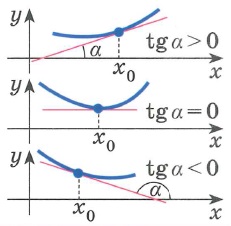
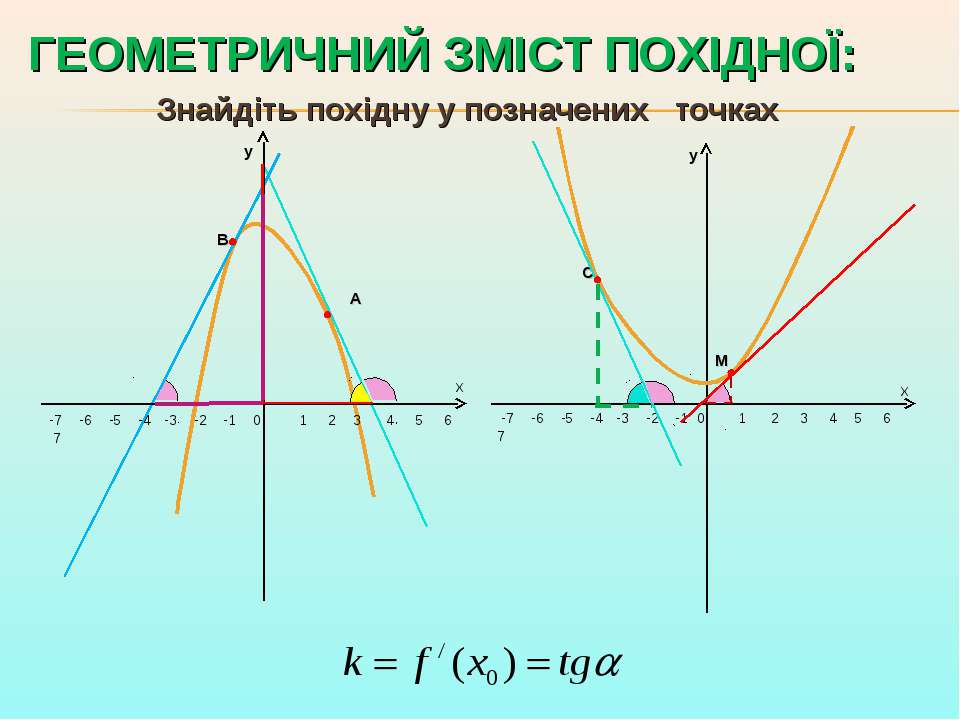
ГЕОМЕТРИЧНИЙ ЗМІСТ ПОХІДНОЇ
Значення похідної в точці xо дорівнює кутовому коефіцієнту
дотичної до графіка функції в точці з абсцисою xо і дорівнює тангенсу кута нахилу цієї дотичної до
осі Ох (кут відраховують від додатного напрямку осі Ох проти годинникової
стрілки).
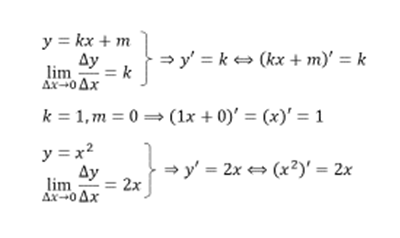

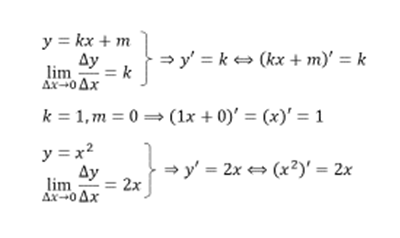

Підведемо підсумки: щоб отримати похідну від функції ƒ необхідна умова щоб функція ƒ була неперервною, але тільки цього не достатньо.
Більшість функцій, що зустрічаються на практиці мають похідні у всіх точках, або майже у всіх точках. Раніше на початку вивчення математичного аналізу, багато математиків припускали, що неперервна функція диференційовна в більшості точок. Для м'яких умов, наприклад якщо маємо монотонну функцію або Ліпшицеву функцію це формулювання справедливе. Проте в 1872 Вейерштрас знайшов перший приклад функції, яка неперервна усюди, але не є диференційованою в жодній точці. Ця функція відома як функція Веєрштраса. В 1931 році Стефан Банах довів, що множина функцій, які мають похідну хоча б в якійсь точці є множина першої категорії в просторі всіх неперервних функцій.[1]
ФІЗИЧНИЙ ЗМІСТ
ПОХІДНОЇ
Похідна характеризує швидкість змінн функції
при зміні аргументу; зокрема,
S = S(t) – функція(формула шляху) залежність пройденого шляху від часу.
v(t) = S'(t) – функція швидкості прямолінійного руху(формула швидкості).
а = v '(t) = S''(t) –
функція прискорення прямолінійного руху (формула швидкості).
Похідна за часом є міра швидкості зміни, що
може застосовуватися до найрізноманітніших фізичних величин. Наприклад, миттєва
швидкість у нерівномірного прямолінійного руху є похідна від функції, яка
виражає залежність пройденого шляху S від чaсу t.
Швидкість світла у вакуумі — абсолютне значення швидкості поширення електромагнітних хвиль у вакуумі. Традиційно позначається літерою латинського алфавіту «c»[3]. Швидкість світла у вакуумі — фізична стала, що не залежить від вибору інерційної системи відліку. Вона відноситься до фундаментальних фізичних сталих, що характеризують не просто окремі тіла чи поля, а властивості простору-часу у цілому. За сучасними уявленнями швидкість світла у вакуумі — гранична швидкість руху і поширення взаємодій.
Точне значення швидкості світла зафіксувала резолюція 1 17-ої Генеральної конференції мір і ваг[4]:
|
|
ФОРМУЛИ ТА ПРАВИЛА ДИФЕРЕНЦІЮВАННЯ
Таблиця похідних елементарних функцій
с' = 0 (с -
стала)
(сf(х))' = сf
'(х)
(с - стала)
Правилo:
Сталий множник можна виносити за знак
похідної/
Приклади: 0' = 0; 6 '
= 0; (- 4)' = 0; (-2(5)0,5) ' = 0.
х ' = 1
Приклади: (х + 4)' = 1 + 0 = 1; (6х) ' = 6; (- 4х)'
= -4; (-2х + 7) ' = -2.
(xа)'= аxа-1 (а -
стала)
Окремі
випадки
(x0,5)' = 0,5x – 0,5 =
1/(2x0,5);
(x2)' = 2x;
(x3)' = 3x2;
(x -1)' = - x -2 =
-1/(x2);
(x -2)' = - 2x -3 =
-2/(x3);
(x1/3)' = (1/3)x – 2/3;
Похідні степеневих функцій
- Степенева функція: Якщо
- ,
де r — будь-яке дійсне число, то
- ,
для будь-яких випадків коли визначена функція. Наприклад, якщо r = 1/2, то
- .
Тут функція визначена тільки для додатних x. Якщо r = 0, це правило повторює правило константи.
Похідні показникових та логарифмічних функцій
- Похідні тригонометричних функцій
Похідна суми
(f + g)' = f ' + g'
Правилo: Похідна суми диференційовних
функцій дорівнює сумі їх похідних.
Похідна добутку
(f(x)∙g(x))' = f '(x)∙g(x) + f(x)∙g'(x)
Похідна частки
(f(x)/g(x))' = [f '(x)∙g(x) – f(x)∙g'(x)]/g2(x),
де g(x) – не дорівнює
нулю.
Похідна складеної функції (функції від
функції)
Якщо
у = f(u) і u = u(х), тобто y = f(u(х)), то
f '(u(х)) = fu'(u)∙ux'(x)
(ех)' = ех
; зокрема (е f(х))'
= f '(х)∙еf(х));
(ах)' = ахlnа, (а > 0 - стала); зокрема (аf(х))' = f '(х)∙аf(х)lnа;
(xх)' = xх(lnx +1), (а > 0 - стала); зокрема (xf(х))' = f '(х)∙xf(х)(lnx +1);
(sinx)' = cosx; зокрема (sinf(x))' = f '(x)∙cosf(x);
(cosx)' = -sinx; зокрема
(cos f(x))' = -f '(x)∙sinf(x);
(tgx)' = 1/cos2x; зокрема (tg f(x))' = f '(x)/cos2 f(x);
(ctgx)' = -1/sin2x; зокрема (ctg f(x))' =
-f '(x)/sin2 f(x);
(arcsinx)' = 1/(1-x2)0,5; зокрема (arcsin f(x))' = f '(x)/(1-f(x)2)0,5;
(arccosx)' =
-1/(1-x2)0,5; зокрема (arccos f(x))' =
-f '(x)/(1-f(x)2)0,5;
(arctgx)' = 1/(1+x2); зокрема (arctg f(x))' = f '(x)/(1+f(x)2);
(arcctgx)' = -1/(1+x2); зокрема (arcctg f(x))' =
-f '(x)/(1+f(x)2).
Приклад А0.
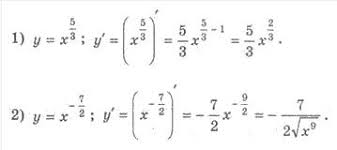
Приклад А1.

Приклад А0.
Приклад А1.

Приклад 1.
(2х4
+ sin35х)' = (2х4)'
+ (sin35х)' = 2(х4)' + 3sin25х•(sin5х)' =
=
2•4х3 + 3sin25х•соs5х•(5х)' = 8х3 + 3sin25х•соs5х•5(х)' =
=
8х3 + 15sin25х•соs5х.
Приклад 2.

Приклад 3-а.

Приклад 3-б.
Приклад 4. Знайти похідні функцій
ПОХІДНІ
ВИЩИХ ПОРЯДКІВ
Для
знаходження похідної будь-якого порядку функції оберненої
пропорційності(простого дробу) користуються формулою:
y(n)(х) = [1/(х+а)](n) = (-1)nn!/(х+а)](n+1).
Для
знаходження похідної будь-якого порядку дробово-лінійної функції користуються
формулою:
y(n)(х) = [(aх+b)/(cх+d)](n) =[ (-1)nn!(bc-ad])/[c2(х+d:c)](n+1)].
Для
знаходження похідної будь-якого порядку функції синуса користуються формулою:
y(n)(х) =( sin ax)(n)= an
sin (ax +
0,5pn).
Для
знаходження похідної будь-якого порядку функції косинуса користуються формулою:
y(n)(х) =(cos
ax)(n)= anсos(ax + 0,5pn).
Для
знаходження похідної будь-якого порядку степеневої
функції користуються формулою:
y(n)(х) =( kxa)(n)= ka(a-1)…(a-n+1)xa-n.
Для
знаходження похідної будь-якого порядку функції експоненти користуються формулою:
y(n)(х) =(kex)(n)= kex.
Для
знаходження похідної будь-якого порядку показникової
функції користуються
формулою:
y(n)(х) =(kax)(n)= kа x(lna)n.
Для
знаходження похідної будь-якого порядку логарифмічної
функції користуються
формулою:
y(n)(х) =(klogax)(n)=(-1) n-1k(n-1)!/xn(lna).
Для
знаходження похідної будь-якого порядку функції
натурального логарифма користуються формулою:
y(n)(х) =(klnx)(n)=(-1) n-1k(n-1)!/xn.
Визначні границі
Визначні границі

В українській мові термін швидкість вживається також не в механічному сенсі для визначення часових характеристик перебігу довільних процесів: наприклад, швидкість хімічної реакції, швидкість нагрівання, швидкість замерзання, швидкість випаровування. Якщо певний процес характеризується залежною від часу величиною , то миттєва швидкість перебігу цього процесу визначається похідною .
Відповідно, середня швидкість за проміжок часу визначається як .
ЕЛЕКТРИЧНИЙ ЗМІСТ ПОХІДНОЇ

ЕКОНОМІЧНИЙ ЗМІСТ ПОХІДНОЇ
ХІМІЧНИЙ ЗМІСТ ПОХІДНОЇ

За зміною ентропії можна визначити напрямок і межу перебігу самодовільного процесу лише в ізольованих системах. Однак на практиці доводиться мати справу й з іншими системами. Для характеристики перебігу процесів у цих системах були введені інші термодинамічні функції.Функцією стану називають характеристичною, якщо на її основі та на основі її похідних можна явно виразити термодинамічні властивості системи і дають змогу визначити напрям і межу того чи іншого спонтанного процесу.Характеристичними функціями є:
- Ентальпія: H = U + PV;
- Вільна енергія (енергія Гелмгольца або ізохорно-ізотермічний потенціал): F = U – TS;
- Термодинамічний потенціал (енергія Гіббса або ізобарно-ізотермічний потенціал):
G = U – TS + PV = H – TS.
Після диференціювання цих виразів одержимо:
dH = dU + PdV + VdP, враховуючи, що dU = ТdS – PdV, тоді
dH = ТdS + VdP; Н = f(S, P), U =f(S, V);
dF = – PdV – SdT; F = f(V, T);
dG = – SdT + VdP = VdP – SdT; G = f(P, T).
Як видно з вибраних форм характеристичних функцій, термодинамічний потенціал Гіббса є найбільш вигідний, оскільки визначається зміною температури і тиску. Якраз ці величини є найбільш простими і зручними для вимірювання. Функції ∆U i∆H також є термодинамічними потенціалами, бо їх зменшення при відповідних сталих дорівнює максимальній корисній роботі.
Ізохорний і ізобарний потенціали є функціями стану, і їх використовують для вирішення питання напрямку процесу в умовах термодинамічної рівноваги. Якщо ∆F і ∆G дорівнюють нулю, то система перебуває в рівновазі, якщо ∆F < 0 і ∆G < 0, то процес відбувається самодовільно з перетворенням енергії у корисну роботу. У випадку, коли ∆F > 0 і ∆G > 0, процес несамочинний, зміна стану системи відбувається тільки при використанні зовнішньої роботи. Так само як енергія Гельмгольца так і енергія Гіббса характеризують працездатність системи і визначають ту частину енергії, яка в ізохорно-ізотермічному та ізобарно-ізотермічному процесах перетворюється у роботу.
Для розрахунку зміни функцій Гіббса і Гельмгольца в результаті хімічних реакцій найчастіше застосовують рівняння Гіббса-Гельмгольца в вигляді:
ΔG = ΔН – TΔS;
ΔF = ΔU – TΔS.
Для обчислень за останніми рівняннями використовують табличні значення стандартних ентальпій утворення та згоряння речовин, а також їх абсолютних ентропій.
Термодинаміка хімічної рівноваги хімічний потенціал
Часткові похідні від інших термодинамічних потенціалів (при відповідних сталих) дорівнюють хімічному потенціалу компонента:

Таким чином, хімічний потенціал даної речовини рівний частинній похідній від будь-якого термодинамічного потенціалу даної фази до числа молів даної речовини при умові, що інші термодинамічні параметри і число молів решти речовин залишаються сталими.
Хімічний потенціал компонента залежить від температури, природи компонента та його вмісту в системі.
Для 1 моль ідеального газу за Т = const маємо:
Інтегруючи це рівняння, отримуємо:
G = RT ln p + const.
За стандартних умов const = G°, деG° – стандартна енергія Гіббса. Отже:
G = G0+ RT ln p.
Для компонента суміші ідеальних газів:
µі=µ0і+ RT lnрi,
де µ0і– стандартний хімічний потенціал, а рi– парціальний тиск компонентаі.
Для ідеальних розчинів:
µі=µ0і+ RT lnсi,
де сi – концентрація компонента в розчині.
Для реальних розчинів концентрацію замінюють активністю:
µі=µ0і+ RT lnаi.
Поняття про активність було введено Льюїсом. Активність –це величина, підстановка якої замість концентрації у термодинамічні рівняння робить їх справедливими для реальних систем.
Активність дорівнює добутку концентрації на коефіцієнт активності:
ai= ci∙ yi або ai= ci∙ γi,
де уi і γi –відповідно молярний і моляльний коефіцієнти активності.
Хімічний потенціал є функцією, що визначає напрямок і межі довільного переходу даного компонента з однієї фази в іншу при відповідних перетвореннях (шляхом випаровування, розчинення, кристалізації і взаємодії).
Загальною умовою можливого перебігу довільного процесу є нерівність
а стану рівноваги відповідає рівність
де µ – хімічний потенціал; dn – зміна кількості молів речовини.



 ,
, ,
, .
.












