Розв’язати рівняння з двома невідомими х та у на множині дійсних чисел: ху=х.
Розв’язання.
ху-х=0;
(ху-1-1)х=0;
х=0; або ху-1-1=0.
Якщо розглядати два випадки:
1)вважати,що існує число: 00=1;
2)вважати, що не існує числа 00.
Для другого випадку, отримаємо:
(х;у)=(0; а), де а – не одиничне дійсне число.
(х;у)=(1; а), де а – дійсне число.
Для першого випадку, отримаємо:
(х;у)=(1; а), де а – дійсне число
(х;у)=(0; а), де а – дійсне число
Розглянемо окремі випадки. Якщо х=1, то зрозуміло, що рівність 1у=1 виконується, якщо у – дійсне число. Маємо розв’язок: (х;у)=(1; а), де а – дійсне число.
Якщо х=-1, то зрозуміло, що рівність (-1)у=-1 виконується для окремих раціональних чисел, а саме, якщо у =(2k-1)/(2n-1) раціональне число, де k-ціле число, n – натуральне число.
Маємо розв’язок: (х;у)=(-1; (2k-1)/(2n-1)), де k-ціле число, n – натуральне число.
Якщо у=-1, то зрозуміло, що рівність (х)-1=х виконується для дійсних чисел, а саме, якщо х дійсне ненульове число. Маємо розв’язок: (х;у)=(а; -1), де а>0 або а<0.
Якщо у=1, то зрозуміло, що рівність (х)1=х виконується для всіх дійсних значень х. Маємо розв’язок: (х;у)=(а; 1), де а – дійсне число.
Якщо у=0, то зрозуміло, що рівність (х)0=х виконується для значенння х=1. Маємо розв’язок: (х;у)=(1; 0), де а – дійсне число.
Показникові рівняння
вигляду ax+bx=c
Вважаєммо, що у рівнянні ax+bx=с
невідоме дійсне значення х,
відомі дійсні додатні значення a, b, c.
Дослідження.
Рівняння вигляду ax+bx=c завжди має один розв'язок, якщо а>1, b>1
бо ліва частина рівняння - це строго монотонна функція, f(x)=ax+bx якщо а>1, b>1
а права частина рівняння - це постійна додатна функція g(x)=c+0*x, c>0.
Виконати заміну,
нехай bx=at,
xlnb=tlna
t = xlnb/lna;
Рівняння змінить вигляд:
ax+at=c
ax+axlnb/lna =c
Винести за дужки множник ax
ax(1+axlnb/lna-x) =c
ax=c/(1+axlnb/lna-x)
А далі ...
Показникові рівняння
вигляду ax+bx=cx
У рівнянні ax+bx=cx
невідоме дійсне значення х,
відомі дійсні додатні значення a, b, c.
Кожний випадок на числа a, b, c вимагає детального дослідження.
Дослідження. Якщо поділити дане рівняння на cx
(a/c)x+(b/c)x=1
Умова неіснування дійсних розв'язків: Якщо ліва частина рівняння f(x)= (a/c)x+(b/c)x
строго монотонна і строго більша за одиницю, то дійсних розв'язків не існує.
У рівнянні ax+bx=cx
невідоме дійсне значення х,
відомі дійсні додатні значення a, b, c.
Дослідження.
Виконати заміну.
1)якщо bx=at, то
xlnb=tlna
t = xlnb/lna;
2)якщо сx=ap, то
xlnc=plna
p = xlnc/lna;
Рівняння змінить вигляд:
ax+at=ap;
ax+at-ap=0;
ax+axlnb/lna
- axlnc/lna =0;
Винести за дужки множник ax
ax(1+axlnb/lna-x-
axlnc/lna-x) =0;
ax =0 або 1+axlnb/lna-x- axlnc/lna-x=0;
Вважаємо, що виконується умова: a, b, c – це додатні
дійсні числа:
Умова існування дійсних розв'язків:
Якщо графіки показникових функцій:
F(x)=1+ax(lnb/lna-1);
G(x)= ax(lnс/lna-1)
мають точку перетину,
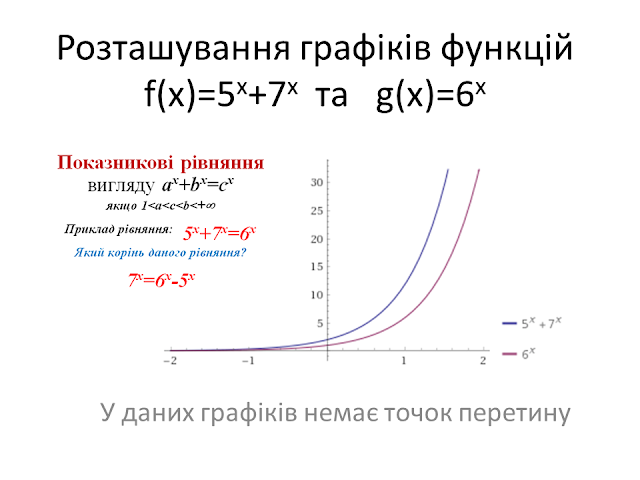
то рівняння ax+bx=cx має дійсні корені.
Якщо графіки показникових функцій:
F(x)=1+ax(lnb/lna-1);
G(x)= ax(lnс/lna-1)
не мають точку поретину,
то рівняння ax+bx=cx дійсних коренів
немає.
Приклади.
1)(1/2)x+(1/3)x=0; дійсних розв’язків не має.
2)(1/2)x+(1/3)x=5/6; звідси х=1.
3)(1/2)x+(1/3)x=2; звідси х=0.
4)(1/2)x+(1/3)x=1;
Розв’язання. Експериментуємо таким чином:
((1/2)0,5x+(1/3)0,5x)2=
=((1/2)x+2(1/2)0,5x(1/3)0,5x+ (1/3)x)=
=1+2(1/2)0,5x(1/3)0,5x=1+2(1/2)0,5(1/3)0,5(1/6)x
(((1/2)0,5x+(1/3)0,5x)(1/6)-0.5x)2=1+2(1/2)0,5(1/3)0,5
((3)0,5x+(2)0,5x)2=1+2(1/2)0,5(1/3)0,5 (*)
((3)0,5x-(2)0,5x)2=1-2(1/2)0,5(1/3)0,5 (**)
((3)0,5x+(2)0,5x)2((3)0,5x-(2)0,5x)2=
((3)x-(2)x)2=
=(1+2(1/2)0,5(1/3)0,5)(1-2(1/2)0,5(1/3)0,5) =
=1-4*0,5*(1/3)=1-2/3=1/3
((3)x-(2)x)2=1/3
((3)x+(2)x)2=1
Отримаємо:
x=1-((5/6)ln(5/6))( (1/2)ln(1/2) +(1/3)ln(1/3))-1.
Показниковими називають рівняння в яких невідома величина міститься в показнику степеня, при цьому основа степеня не містить невідомої величини. Саме просте показникове рівняння ax=b розв'язують логарифмуванням x=log[a](b).
При розв'язуванні показникових рівнянь використовують властивість показників: якщо рівні вирази з однією і тією ж основою, то рівні показники степені, або основа дорівнює одиниці.
З рівності

слідує x=y або a=1.
З рівності
слідує x=y або a=1.
Деякі рівняння потребують заміни змінної, що веде до розв'язування степеневого рівняння. Для прикладу рівняння

легко зводиться до квадратного, якщо зробити заміну
3x=y
легко зводиться до квадратного, якщо зробити заміну
3x=y
При цьому вихідне рівняння набуде вигляду

Після його розв'язку потрібно повернутися до заміни і розв'язати отримане рівняння.
На цьому необхідний теоретичний матеріал закінчується і переходимо до розгляду поширених прикладів.
Одним з основних методів розв'язування показникових рівнянь полягає в тому, що рівняння за допомогою рівносильних перетворень намагаються звести до виду
Останнє рівняння рівносильне рівнянню:
Приклад 1. Розв'язати рівняння:
Відповідь. -1.
Приклад 2. Розв'язати рівняння: 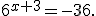
Дане рівняння коренів немає, оскільки ліва частина 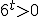 для всіх
для всіх 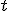 , а права -36<0.
, а права -36<0.
Відповідь. коренів немає.
Якщо в лівій і правій частинах показникового рівняння стоять тільки добутки, частки, корені або степені, то доцільно за допомогою основних формул спробувати записати обидві частини рівняння як степені з однією основою.
Приклад 3. Розв'язати рівняння:
Відповідь. 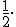
Якщо в одній частині показникового рівняння стоїть число, а в іншій всі члени містять вираз виду 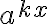 (показники степенів відрізняються тільки вільними членами), то зручно в цій частині рівняння винести за дужки найменший степінь а.
(показники степенів відрізняються тільки вільними членами), то зручно в цій частині рівняння винести за дужки найменший степінь а.
Приклад 4. Розв'язати рівняння:
Відповідь. 2.
Показниковими зазвичай називають рівняння, у яких змінна входить у показник степеня (а основа цього степеня не містять змінної).
Розглянемо найпростіше показникове рівняння
де 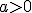 і
і 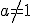 . Оскільки при цих значеннях
. Оскільки при цих значеннях  функція
функція 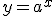 строго монотонна (зростає при
строго монотонна (зростає при 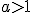 і спадає при
і спадає при 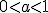 ), то кожного свого значення вона набуває тільки при одному значенні аргументу. Це означає, що рівняння
), то кожного свого значення вона набуває тільки при одному значенні аргументу. Це означає, що рівняння 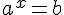 при b>0 має єдиний корінь. Щоб його знайти, досить подати b у вигляді
при b>0 має єдиний корінь. Щоб його знайти, досить подати b у вигляді 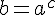 .
.
Очевидно, що 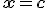 є коренем рівняння
є коренем рівняння 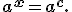
Наприклад, щоб розв'язати рівняння 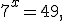 досить подати це рівняння у вигляді
досить подати це рівняння у вигляді 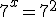 і записати його єдиний корінь
і записати його єдиний корінь 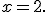
Якщо 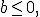 то рівняння
то рівняння 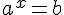 (при a> 0) коренів не має, оскільки
(при a> 0) коренів не має, оскільки 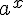 завжди більше нуля. (На графіку пряма
завжди більше нуля. (На графіку пряма 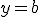 не перетинає графік функції
не перетинає графік функції 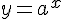 при
при 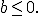 )
)
Наприклад, рівняння 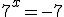 не має коренів.
не має коренів.
Узальнюючи наведені вище міркування стосовно розв'язування найпростіших показникових рівнянь, відзначимо, що при 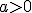 і
і 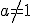 рівняння
рівняння
рівносильне рівнянню
Щоб обґрунтувати цю рівносильність, досить помітити, що рівності (2) і (3) можуть бути правильними тільки одночасно, оскільки функція 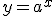 є строго монотонною і кожного свого значення вона набуває тільки при одному значенні аргументу
є строго монотонною і кожного свого значення вона набуває тільки при одному значенні аргументу 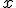 (тобто з рівності степенів (2) обов'язково випливає рівність показників (3)).
(тобто з рівності степенів (2) обов'язково випливає рівність показників (3)).
Отже, усі корені рівняння (2) (які перетворюють це рівняння на правильну рівність) будуть і коренями рівняння (3), та навпаки, усі корені рівняння (3) будуть коренями рівняння (2).
А це й означає, що рівняння (2) і (3) рівносильні.
Отже, у найпростіших випадках при розв'язуванні показникових рівнянь намагаються за допомогою основних формул дій над степенями звести (якщо це можливо) задане рівняння до виду }=a^{g(x)}) .
.
Для розв'язування більш складних показникових рівнянь найчастіше використовують заміну змінної або властивості відповідних функцій.
Зауважимо, що всі рівносильні перетворення рівняння завжди виконуються на його області допустимих значень (тобто на спільній області визначення для всіх функцій, які входять до запису цього рівняння). Але в показникових рівняннях найчастіше областю допустимих значень (ОДЗ) є множина всіх дійсних чисел. У цих випадках, як правило, ОДЗ явно не знаходять і не записують до розв'язання рівняння (див. нижче приклади). Але якщо в процесі розв'язування показникових рівнянь рівносильні перетворення виконуються не на всій множині дійсних чисел, то в цьому випадку доводиться згадувати про ОДЗ .
Приклади розв'язання рівнянь
Приклад 5. Розв'язати рівняння:
Відповідь. 5.
У лівій і правій частинах рівняння стоять тільки добутки, частки, корені або степені. У цьому випадку для зведення рівняння до виду }=a^{g(x)}) спробуємо використати основні формули дій над степенями, щоб записати обидві частини рівняння як степені з однією основою. Слід звернути увагу на те, що
спробуємо використати основні формули дій над степенями, щоб записати обидві частини рівняння як степені з однією основою. Слід звернути увагу на те, що
та 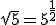 , отже, ліву і праву частини цього рівняння можна записати як степені числа 5.
, отже, ліву і праву частини цього рівняння можна записати як степені числа 5.
Приклад 6. Розв'язати рівняння:
Для перетворення рівняння згадаємо, що всі формули можна використовувати як зліва направо, так і справа наліво, наприклад, для лівої частини цього рівняння скористаємося тим, що ^x=6^x.)
Відповідь. 1.
Приклад 7. Розв'язати рівняння:
Задане рівняння рівносильне рівнянням:
Відповідь. 1.
У лівій частині рівняння всі члени містять вирази виду 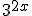 (показники степенів відрізняються тільки вільними членами). У цьому випадку зручно винести за дужки в лівій частині рівняння найменший степінь числа 3, тобто
(показники степенів відрізняються тільки вільними членами). У цьому випадку зручно винести за дужки в лівій частині рівняння найменший степінь числа 3, тобто 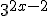 .
.
Приклад 8. Розв'язати рівняння з параметром:
ОДЗ: 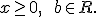
1) При 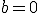 отримуємо рівняння
отримуємо рівняння 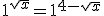 , корені якого - усі дійсні числа з ОДЗ, тобто
, корені якого - усі дійсні числа з ОДЗ, тобто 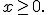
2) При 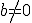 значення
значення 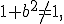 і тоді задане рівняння рівносильне рівнянню
і тоді задане рівняння рівносильне рівнянню 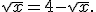
Звідси 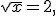 тоді
тоді 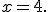
Відповідь. 1) при 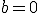 ,
, ;)
2) при 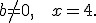
Це рівняння відносно змінної 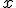 , яке містить параметр
, яке містить параметр 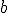 . Аналізуючи основу степенів у цьому рівнянні, робимо висновок, що при будь-яких значеннях
. Аналізуючи основу степенів у цьому рівнянні, робимо висновок, що при будь-яких значеннях 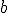 основа
основа 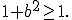 Функція
Функція 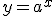 при
при 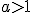 є зростаючою, а при
є зростаючою, а при 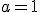 - постійною.
- постійною.
Основа 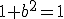 при
при 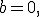 а
а 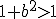 при
при 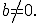
Розглядали кожен із цих випадків окремо, тобто: 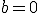 і
і 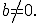
Приклад 1.Розв'язати рівняння

Розв'язок. Перепишемо рівняння в наступному вигляду

Другий доданок розпишемо, як добуток

та зробимо заміну у рівнянні

Вихідне рівняння перетвориться до наступного

Областю допустимих значень буде дійсна множина за винятком точки y=0.
Помножимо залежнысть на y та переносимо выльний член в ліву сторону

Отримали квадратне рівняння, корені якого знаходимо за теоремою Вієта. Не важко переконатися, що вони приймають значення

Повертаємося до заміни, та знаходимо розв'язки


Виконуємо перевірку


Отже обидва розв'язки x=1; x=3 задовольняють рівняння.
Другий доданок розпишемо, як добуток
та зробимо заміну у рівнянні
Вихідне рівняння перетвориться до наступного
Областю допустимих значень буде дійсна множина за винятком точки y=0.
Помножимо залежнысть на y та переносимо выльний член в ліву сторону
Отримали квадратне рівняння, корені якого знаходимо за теоремою Вієта. Не важко переконатися, що вони приймають значення
Повертаємося до заміни, та знаходимо розв'язки
Виконуємо перевірку
Отже обидва розв'язки x=1; x=3 задовольняють рівняння.
Приклад 2. Розв'язати рівняння

Розв'язок. Використовуючи одну з властивостей логарифма записуємо праву сторону рівняння у вигляді

Прирівнявши показники, знаходимо

Отак вигядає правило про рівність показників при рівних осповах.
Прирівнявши показники, знаходимо
Отак вигядає правило про рівність показників при рівних осповах.
Приклад 3. Розв'язати рівняння

Розв'язок. Такого сорту приклади розв'язують логарифмуванням обох сторін, що приводить до зведення показникового рівняння до простого вигляду.


Отримане рівняння відносно змінної розв'язуємо через дискримінант

Корені рівняння набудуть значень



Іншого методу, який би дозволяв аналітично отримати розв'язки Ви не знайдете ні в інтернеті, ні на форумах.
Те що корені отримали громіздкі та ірраціональні - не проблеблема, головне що вони правильно знайдені.
Отримане рівняння відносно змінної розв'язуємо через дискримінант
Корені рівняння набудуть значень
Іншого методу, який би дозволяв аналітично отримати розв'язки Ви не знайдете ні в інтернеті, ні на форумах.
Те що корені отримали громіздкі та ірраціональні - не проблеблема, головне що вони правильно знайдені.
Приклад 4. Розв'язати рівняння

Розв'язок. Виконаємо деякі перетворення з показниками, щоб спростити рівняння

Еквівалентні значення підставимо у рівняння, в результаті отримаємо

Виконуємо заміну змінних у показниковому рівнянні

З врахуванням заміни переходимо до обчислень квадратного рівняння


Знаходимо диискримінант

Отримане значення підставляємо у формулу коренів


На цьому обчилення не завершені. Повертаємося до заміни змінних та знаходимо розв'язки показникового рівняння

Тепер лише можна онстатувати, що завдання розв'язано.
Еквівалентні значення підставимо у рівняння, в результаті отримаємо
Виконуємо заміну змінних у показниковому рівнянні
З врахуванням заміни переходимо до обчислень квадратного рівняння
Знаходимо диискримінант
Отримане значення підставляємо у формулу коренів
На цьому обчилення не завершені. Повертаємося до заміни змінних та знаходимо розв'язки показникового рівняння
Тепер лише можна онстатувати, що завдання розв'язано.
Приклад 5.Розв'язати рівняння

Розв'язок. Такого типу рівняння розв'язують за сталою основою. За основу класично беруть 10, однак, якщо взяти іншу (для даного прикладу 5 або 9) то розв'язок прийме компактніший вигляд.
Розглянемо обидва методи.
1. Прологарифмуємо обидві частини показникового рівняння

Розкриваємо дужки та групуємо доданки при невідомих. Вкінці виражаємо шукану веичину


Отакий цікавий результат.
Розглянемо обидва методи.
1. Прологарифмуємо обидві частини показникового рівняння
Розкриваємо дужки та групуємо доданки при невідомих. Вкінці виражаємо шукану веичину
Отакий цікавий результат.
2. Прологарифмуємо обидві частини рівності за основою 9

Групуючи доданки, що містять змінну, отримаємо


Обидва методи достатньо швидкі та ефективні. Відповіді хоч і не подібні, проте на інженерному калькуляторі чи будь-якому математичному пакеті можете переконатися, що вони рівні.
Групуючи доданки, що містять змінну, отримаємо
Обидва методи достатньо швидкі та ефективні. Відповіді хоч і не подібні, проте на інженерному калькуляторі чи будь-якому математичному пакеті можете переконатися, що вони рівні.
Приклад 6. Розв'язати рівняння

Розв'язок. Такого роду завдання розв'язують за наступною схемою. Показникове рівняння перетворюють до наступного вигляду

Усі доданки розділяємо на величину , щоб звести до дробового вигляду
, щоб звести до дробового вигляду

Після цього виконуємо заміну змінних

Далі Ви можете повправлятися самостійно. Якщо не маєте можливості, то перетворємо за наведеною вище схемою

Множимо на змінну та розв'язуємо квадратне рівняння відносно нової змінної


Дискримінант приймає нульове значення, отже корені рівняння співпадають

Повертаємося до заміни та розв'язуємо простеньке показникове рівняння


Хто не згідний, що дане рівняння просте, можете поставити "лайк" вкінці уроку.
Отримали єдиний розв'язок x=2.
Використовуйте наведену схему до подібних завдань і гарантовано отримаєте вірний результат.
Усі доданки розділяємо на величину
Після цього виконуємо заміну змінних
Далі Ви можете повправлятися самостійно. Якщо не маєте можливості, то перетворємо за наведеною вище схемою
Множимо на змінну та розв'язуємо квадратне рівняння відносно нової змінної
Дискримінант приймає нульове значення, отже корені рівняння співпадають
Повертаємося до заміни та розв'язуємо простеньке показникове рівняння
Хто не згідний, що дане рівняння просте, можете поставити "лайк" вкінці уроку.
Отримали єдиний розв'язок x=2.
Використовуйте наведену схему до подібних завдань і гарантовано отримаєте вірний результат.
Приклад 7. Розв'язати рівняння

Розв'язок. На перший погляд рівняння досить складне і невідомо як його спрощувати, проте схема розв'язування даного прикладу та йому подібних досить проста та зрозуміла.
Виконаємо над рівнянням перетворення показників

Далі необхідно показникову залежність перетворити до квадратного рівняння



Повірте, що таке побачити по умові і виконати дуже важко для початківця, але з практикою Ви навчитеся розрізняти рівняння і яку підстановку слід застосовувати.
Виконаємо заміну змінних
та переписуємо рівняння у вигляді

Обчислюємо дискримінант вадратного рівняння

та корені рівняня

Повертаємося до зробленої заміни та знову отримуємо показникове

Ох і приклад дістався. Одні показникові рівняння розв'язуються через інші.
Отримане рівняння зводимо до квадратного, виконавши заміну
В результаті прийдемо до квадратичної залежності

Розв'язуємо через дискримінант


Повертаємося до заміни і визначаємо змінну x знову ж таки - з показникового рівняння (логарифмуванням)

Друге значення розглядати не будемо, оскільки воно від'ємне, а показникова функція
розглядати не будемо, оскільки воно від'ємне, а показникова функція  всюди додатна.
всюди додатна.
Не забуваємо, що в нас є ще один корінь рівняння, який може внести свій вклад в кінцеву відповідь.
Розв'язуємо другу половину завдання

Використовуючи попередню заміну, отримаємо

Через дискримінант

знаходимо корені рівняння

Перший корінь має зміст, другий – від'ємний і не підходить.

Отримали два розв'язки показникового рівняння

Отаке чудернацьке рівняння можуть придумати математии, щоб завалити Вас на тестах чи екзаменах.
Тож ставтися до навчання відповідально і вдосконалюйте знання від простих до складних завдань.
Виконаємо над рівнянням перетворення показників
Далі необхідно показникову залежність перетворити до квадратного рівняння
Повірте, що таке побачити по умові і виконати дуже важко для початківця, але з практикою Ви навчитеся розрізняти рівняння і яку підстановку слід застосовувати.
Виконаємо заміну змінних
та переписуємо рівняння у вигляді
Обчислюємо дискримінант вадратного рівняння
та корені рівняня
Повертаємося до зробленої заміни та знову отримуємо показникове
Ох і приклад дістався. Одні показникові рівняння розв'язуються через інші.
Отримане рівняння зводимо до квадратного, виконавши заміну
В результаті прийдемо до квадратичної залежності
Розв'язуємо через дискримінант
Повертаємося до заміни і визначаємо змінну x знову ж таки - з показникового рівняння (логарифмуванням)
Друге значення
Не забуваємо, що в нас є ще один корінь рівняння, який може внести свій вклад в кінцеву відповідь.
Розв'язуємо другу половину завдання
Використовуючи попередню заміну, отримаємо
Через дискримінант
знаходимо корені рівняння
Перший корінь має зміст, другий – від'ємний і не підходить.
Отримали два розв'язки показникового рівняння
Отаке чудернацьке рівняння можуть придумати математии, щоб завалити Вас на тестах чи екзаменах.
Тож ставтися до навчання відповідально і вдосконалюйте знання від простих до складних завдань.









Немає коментарів:
Дописати коментар